Analisis persamaan secara umum untuk menemukan suatu fungsi maksimum dan minimum.
menentukan jarak suatu jarak atara dua titik
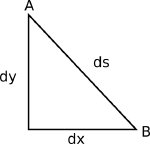
Meminimalkan jarak lintasan#
$$ \begin{align} \Iota &= \int_{x_1}^{X_2} ds \newline \Iota &= \int_{x_1}^{X^2} \left( \sqrt{1+\frac{dy^2}{dx^2}} \right) dx \newline \Iota &= \int_{x_1}^{x^2}\left( 1+ y’^2 \right)^\frac{1}{2} \newline y’ &= \frac{dy(x)}{dx} \newline y &= extermal \end{align} $$
$$ \begin{align} Y &= y(x)+ \epsilon \eta(x) \newline \end{align} $$ dimana: $$ \eta(x) \vert_{A_1} = \eta \vert_{A_2} =0 $$
Meminimalkan waktu tempuh#
$$ \begin{align} \Iota &= \int_{x_1}^{x_2}t \ ds \newline \Iota &=\int_{x_1}^{x_2} \frac{\sqrt{1+y’^2}}{V} \newline \Iota &=\int_{x_1}^{x_2}\frac{\sqrt{1+y’^2}}{\sqrt{2g (y_1-y_2)}}dx \end{align} $$
Meminimalkan Energi#
$$ \begin{align} \Iota &= \int_{x_1}^{x_2}mghds \newline &= \int_{x_1}^{x_2}\rho Agy \ ds \newline &= \int_{x_1}^{x_2}\rho A gy (\sqrt{1+y'2}) dx \newline &= \rho A g\int_{x_1}^{x_2}y (\sqrt{1+y'2}) dx \newline \end{align} $$
Meminimalkan Lagraian#
$$ \begin{align*} L(x,y,y’)&= T-V \newline &= \frac{1}{2}mv^2-mgy \newline &= \frac{1}{2}m\frac{dy^2}{dt}-mgy \newline &= \frac{1}{2}my’^2-mgy \newline \end{align*} $$ $$ \begin{equation} \Iota=\int_{x_1}^{x_2}L(x,y,y’)dx \end{equation} $$
Persamman Euler-Lagraian#
$$ \begin{equation} \frac{d}{dx}\frac{\partial F}{\partial y’}-\frac{\partial F}{\partial y}=0 \end{equation} $$


